[백준 python] 1432번 그래프 수정
레벨: 플레티넘5
언어: 파이썬
📑풀이 과정
이 문제는 정글 ㅇㅎㅈ님의 설명을 듣고 이해한 문제이다. 감사합니다ㅎㅎ
V1 → V2로 연결된 간선이 있을때, V2의 번호는 V1보다 커야한다.
위 조건으로 간선의 번호를 바꾸면 위상정렬 시 노드의 번호 순서(오른차순)으로 나와야한다는 말이다.
문제에 대한 이해
예시) 1번 그림 표현
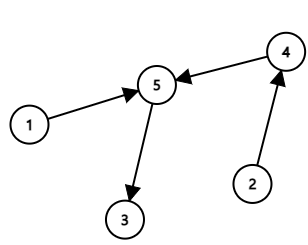
위 예시를 위상정렬하면 1 2 4 5 3 이 나오고
위 예시를 위상 정렬시 1 2 3 4 5 로 출력하려면 아래와 같이 노드를 바꾸면 된다.
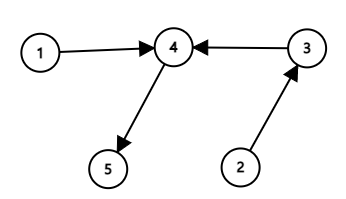
첫번째 그림의 노드위치가 아래로 바뀌면서
1 → 1
2 → 2
3 → 5
4 → 3
5 → 4
으로 바뀌게 되고
예시 답인 1 2 5 3 4 가 나오게 된다.
그리고 그래프에서 사이클이 발생하면 위상정렬이 안되기에 -1의 값을 출력하면 된다.
여기까지가 문제에 대한 이해였다.
이렇게 이해하고 위상 정렬시 Queue에서 값이 나오는 순서대로 answer배열에 저장하고 제출하면 틀렸습니다.를 보게 될 것이다.
문제의 핵심
이 문제의 핵심은 답이 여러 개일 경우에는 사전 순으로 제일 앞서는 것을 출력한다. 이 부분이다.
위 처럼 1번부터 최소힙을 사용하면 반례가 생긴다.
# 반례
4
0011
0000
0000
0100기존 위의 알고리즘: 1 4 2 3
문제의 정답: 1 3 4 2
기존 알고리즘 결과도 위상 정렬시 1 2 3 4 순으로 출력이 되지만 사전 순으로 출력시 아래의 답이 먼저이기 때문에 틀렸습니다 를 얻게 된다.
이 문제를 풀기위해선 indegree가 아닌 outdegree를 사용해서 answer의 배열을 1부터 넣지 않고 N부터 넣어가야한다.
- outdegree를 사용
- 최대힙을 사용
- answer를 N부터 대입
outdegree를 사용하는 건 간선의 방향을 뒤집어 주면된다.
위 그림에서 아래그림처럼 간선을 변경하면 된다.
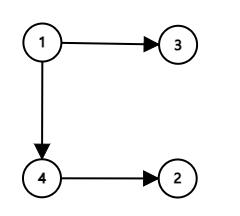
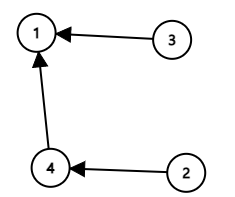
outdegree와 최대힙 사용 이유
이 부분이 이해가 가장 되지 않았다. 왜 간선의 방향을 바꾸고 최대힙을 써야하는지 말이다.
일단 사전 순 정렬을 할 때 단어가 하나만 있다면 오름차순으로 정렬하면 된다.
ㄷㄴㄱㄹ 라면 오름 차순으로 ㄱㄴㄷㄹ이 된다.
하지만 값이 (이름, 나이) 처럼 2개가 있을 때 이름 순으로 정렬하되 이름이 같으면 나이 순으로 정렬하라는 문제에서 순서대로 이름, 나이순으로 정렬하면 반례가 발생한다.
이때는 우선순위가 낮은것부터 정렬 후 우선순위가 높은 것으로 정렬해야한다.
우선순위가 낮은 나이를 먼저 정렬하고 이름을 정렬하면 반례가 발생하지 않는다.
예시)
| 입력값 | 이름 정렬 후 | 나이 정렬 | 기대 값 |
| (ㄴ,20) | (ㄱ, 25) | (ㅎ, 10) | (ㄱ, 25) |
| (ㄴ,15) | (ㄴ, 20) | (ㄴ, 15) | (ㄴ, 15) |
| (ㄱ,25) | (ㄴ, 15) | (ㄴ, 20) | (ㄴ, 20) |
| (ㅎ,10) | (ㅎ, 10) | (ㄱ, 25) | (ㅎ, 10) |
| 입력값 | 나이 정렬 후 | 이름 정렬 | 기대 값 |
| (ㄴ,20) | (ㅎ, 10) | (ㄱ, 25) | (ㄱ, 25) |
| (ㄴ,15) | (ㄴ, 15) | (ㄴ, 15) | (ㄴ, 15) |
| (ㄱ,25) | (ㄴ, 20) | (ㄴ, 20) | (ㄴ, 20) |
| (ㅎ,10) | (ㄱ, 25) | (ㅎ, 10) | (ㅎ, 10) |
우선 순위순으로 정렬의 순서를 바꿨을 뿐인데 결과 값이 완전히 달라진다.
우리 문제에서는
앞쪽이 우선 순위가 높고, 뒤쪽 우선 순위가 낮다.
그리고 사전순으로 출력을 위해서
앞쪽은 낮은 수, 뒤쪽 높은 수로 되어야한다.
그렇기에 우선순위를 낮은 순으로 정렬하기 위해 간선의 방향을 바꿔서 진행
뒤는 높은 수가 되어야 하기에 최대힙으로 진행한다.
import heapq
import sys
input = sys.stdin.readline
def topology_sort():
q = []
for i in range(1, n+1):
if indegree[i] == 0:
# heapq.heappush(q,i)
heapq.heappush(q,-i)
N = n
while q:
now = -heapq.heappop(q)
answer[now] = N
for i in node[now]:
indegree[i] -= 1
if indegree[i] == 0:
heapq.heappush(q, -i)
# N+=1
N -=1
n = int(input())
node = [[] for _ in range((n+1))]
indegree = [0] * (n+1)
# 인접행렬 입력 ->인접리스트로 변경
for v in range(1, n+1):
temp = [0]+ list(map(int, input().strip()))
for i in range(1, n+1):
if temp[i] == 1:
node[i].append(v)
indegree[v] += 1
answer = [0]*(n+1)
topology_sort()
if answer.count(0) > 1:
print(-1)
else:
print(*answer[1:])'지난 글 모음' 카테고리의 다른 글
| [week05] sw정글 사관학교 5주차 회고 (0) | 2022.05.02 |
|---|---|
| [week03 & week04] 3,4 주차 sw정글 회고 (4) | 2022.04.24 |
| [백준 python] 10000번 원 영역 (2) | 2022.04.10 |
| [week02] SW정글 2주 차 회고 (1) | 2022.04.10 |
| [백준 python] 10819번 차이를 최대로 -재귀, 순열 풀이 (0) | 2022.04.04 |